El principio de identidad
Si yo me acerco a usted y le digo algo como (1)
(1) todo objeto es idéntico a sí mismo.
Probablemente piense que me he vuelto loco y digo sandeces o bien no entendería nada o, tal vez, vería claro que (1) es una trivialidad. Trivialidad o no, (1) es la versión ontológica del principio de identidad. Lo que dice es que cada una de las cosas que pueblan el mundo es esa misma cosa. En sí mismo, si se quiere tomar demasiado en serio es una auténtica trivialidad. No obstante, en el tráfico lingüístico se pueden oír algunas versiones particulares del principio de identidad, tales como «la vida es la vida».
El principio de identidad también tiene una versión lógica, (2)
(2) (x)(x = x)
(2) es la versión del principio o ley de identidad en lógica de predicados. La traducción de (2) al lenguaje natural dice que «para todo x, x es igual a x. (2) puede ser utilizado en cálculos lógicos para extraer fórmulas bien formadas a partir de fórmulas bien formadas.
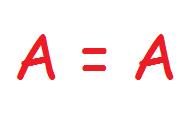
Principio de identidad formulado en el lenguaje de la lógica proposicional
Kripke y la necesidad de la identidad
En el transcurso de uno de sus argumentos, Kripke introduce una premisa en la que aparece una nueva formulación de la ley de identidad. Kripke mantiene que, indudablemente, la identidad es necesaria y en el curso de su argumentación introduce la siguiente versión de la ley de identidad:
(3) (x)L(x = x)
Lo que dice (3), traducido al lenguaje natural es que «para todo x, necesariamente x es igual a x». Kripke utiliza (3) para llegar a su conclusión, según la cual, en su versión informal, «para todo x, para todo y, si x es igual a y entonces necesariamente x es igual a y. Esta tesis fue defendida originalmente por Ruth Barcan Marcus. La fórmula es la siguiente:
(4) (x)(y) [(x = y) –> L(x = y)]
El argumento de Kripke es el siguiente: para él todo objeto es idéntico a sí mismo en todo mundo posible en el que tal objeto exista. Con un ejemplo, yo soy yo en todo mundo posible en el que yo exista. Están los mundos M1, M2 y M3 (no necesitamos más). Yo existo en M1 y M2, pero no en M3. Así que lo que (4) dice es que yo en M1 y yo en M2 somos la misma cosa. Esto es así, dice Kripke, porque estrictamente hablando solo existe un mundo, este, y lo que llamamos «mundos posibles» son estipulaciones contrafácticas que hacemos sobre el mundo actual. Me encuentro una pera, la pruebo y está ácida. Aún no ha madurado. Pienso (5)
(5) esta pera podría estar madura.
La pera, de hecho, está verde, pero estipulamos una situación contrafáctica en la que esa mismísima pera y no otra estaría madura. Eso es un mundo posible y para que (4) sea verdadera, (3) ha de serlo, pues a (4) llega Kripke a partir de (6)
(6) (x)(y)(x = y) –> [L(x = x) –> L(x = y)]
ya que (3) nos permite eliminar L(x = x) en (6). Y así obtenemos (4)
La debilidad de la tesis de que la identidad es necesaria
La debilidad de (3) está en que para que sea verdadera tiene que ser correcta la intuición kripkeana respecto de los mundos posibles. Es decir, existen otras concepciones alternativas que hacen falsa (3), como la de David Lewis, según la cual los mundos posibles existen, son como otros planetas (es decir, podemos hablar de otros mundos posibles como hablamos de otros planetas o ciudades). Algunos de ellos se parecen al nuestro. Los objetos de aquí, sin embargo, no son idénticos a los de allí, no son los mismos que los del resto de mundos posibles. Son contrapartidas y hay una semejanza cualitativa entre unos y otros. Por ejemplo, podría haber un mundo posible en el que una contrapartida mía está escribiendo una contrapartida de este artículo, solo que esta contrapartida mía tiene el pelo verde y alas de polilla. Es un mundo semejante a este, en el que alguien desempeña allí un papel similar al que desempeño yo aquí, sin embargo ese alguien no soy yo, solo nos parecemos.
