La lógica clásica

¿Qué es la lógica clásica? Según algunos la lógica clásica estaría constituida por un conjunto de cálculos lógicos equivalentes al cálculo presentado por Bertrand Russell y Alfred N. Whitehead en sus Principia Mathematica (1910-1913). Otro punto de vista es el que dice que la lógica clásica es aquella que se desarrolla desde Aristóteles hasta las aportaciones de Alfred Tarski, hacia mediados de los años 30 del siglo XX. Cualquiera de las dos definiciones nos viene bien, pues resulta que todos los sistemas lógicos a los que llamamos «lógica clásica» comparten la propiedad de ser equivalentes al cálculo de Principia y, a su vez, todos ellos son producto y han nacido gracias a las aportaciones realizadas por los lógicos desde Aristóteles a Tarski. Dicho esto, pasamos a profundizar en la lógica clásica.

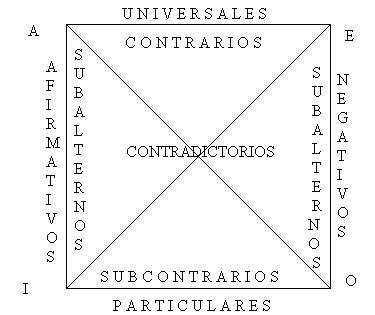
Cuadro de la oposición de los juicios. Se utilizaba para el estudio de las relaciones formales entre los distintos tipos de juicios.

Características de los cálculos que constituyen la lógica clásica

Varios son los cálculos que caen bajo el dominio de la lógica clásica, pero entre ellos destacan la lógica proposicional, la lógica de predicados de primer orden y la lógica de predicados de segundo orden. Todos ellos comparten una serie de características comunes, las cuales a continuación enumeramos.

1. Son lógicas bivalentes, esto es, solo operan con dos valores de verdad: verdadero y falso.

2. Todas ellas se basan en el principio de identidad, el de no contradicción, en el principio del tercero excluido y en el principio de explosión (ex falso quodlibet).

3. Son, como hemos dicho, equivalentes al cálculo de Principia y, por lo tanto, equivalentes entre sí.

Proceso de formación de la lógica clásica

La lógica clásica, los sistemas lógicos a los que clasificamos como tal, no nació como un corpus cerrado, sino que se fue construyendo a lo largo de la historia. Así, la lógica clásica nace con Aristóteles, con su teoría del silogismo categórico, expuestas en los Primeros analíticos. Allí el estagirita introduce de forma implícita las nociones que van a constituir esta ciencia, a saber, las nociones de validez, la de deducción y la de inferencia.

Por su parte, los lógicos megáricos y estoicos identificaron las conectivas y algunas reglas de inferencia, dándole el primer empujón de la historia al cálculo deductivo. Destaca la introducción del antepasado de nuestro condicional material, en aquel entonces conocido como condicional filónico, y la del antepasado de nuestra implicación estricta, llamado en aquella época condicional diodórico. También introdujeron las reglas de inferencia asociadas al condicional material: Modus Ponens y Modus Tollens.

Tras los avances de los lógicos estoicos y de los megáricos, la lógica queda estancada, salvo por la teoría de la consequentia desarrollada durante la Edad Media, sobre todo a partir de Boecio. Ya en el siglo XVII Leibniz publica Ars combinatoria. En esta obra Leibniz plantea la creación de un lenguaje artificial para expresar el pensamiento puro sin la interferencia de las vaguedades propias del lenguaje ordinario. Por su parte, en el siglo XIX Bolzano introduce algunas ideas que influyeron en la formación de la lógica.

Y es en el siglo XIX cuando la lógica clásica va a experimentar su mayor evolución, cuando sea matematizada. Los inicios de la matematización de la lógica nos los encontramos en las obras de Augustus De Morgan y de George Boole, quienes comienzan a utilizar fórmulas algebraicas para expresar relaciones lógicas. No obstante, no es hasta finales del siglo XIX, cuando las bases definitivas de la lógica clásica quedan sentadas, alcanzando, asimismo, un alto grado de matematización. Este espectacular avance se produce cuando Gottlob Frege publica Begriffschriff (Conceptografía) en 1879. Es la primera vez en la historia en la que un sistema lógico aparece totalmente formalizado. La propuesta de Frege será perfeccionada por Russell y Whitehead en Principia Mathematica.

Finalmente hay que añadir el programa formalista de Hilbert, comenzado en 1899, con la introducción del concepto de metamatemática como nombre de una disciplina formal que estudia desde un metalenguaje el lenguaje objeto de la matemática. Por último hay que introducir las contribuciones al campo de la semántica de la lógica realizadas por Alfred Tarski, concretamente a sus investigaciones sobre el concepto de verdad (1933) y el de consecuencia lógica (1936).