Curso de Lógica (XVI): introducción a la lógica de predicados
Visto el lenguaje de la lógica proposicional y la teoría de conjuntos, vamos a pasar ya a nuestra parte culminante de nuestro curso de Lógica. Se trata de la lógica de predicados. Dado que en lógica nos interesa la validez de los argumentos, necesitamos herramientas formales que nos ayuden a ello. Por otra parte, la lógica proposicional resulta insuficiente para dar cuenta de la validez de muchos argumentos. Por ejemplo, el argumento (1)
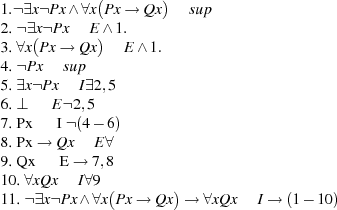
Una deducción en lógica de predicados. Más adelante aprenderemos a hacer deducciones de este tipo.
(1) Todas las aves tienen alas, Piolín es un ave; por tanto Piolín tiene alas.
La lógica proposicional no puede dar cuenta de la validez de este argumento, en la medida en que trata cada uno de los enunciados que forman (1) como si fueran simples. La formalización de (1) es la siguiente:
p
q
____
(1) es un argumento que es válido, pero cuando lo formalizamos al lenguaje de la lógica proposicional obtenemos un argumento inválido. Esto se debe a que la validez de (1) depende de la estructura de los enunciados que lo componen. Y esto es algo que con el lenguaje de la lógica proposicional no podemos representar, puesto que no considera la estructura de los enunciados de este tipo. Es por esta razón que para estudiar la validez de argumentos como (1) necesitamos un aparato formal más preciso que el proporcionado por el lenguaje de la lógica proposicional. Estas herramientas nos las da la lógica de predicados.
El lenguaje de la lógica de predicados
La lógica proposicional no es solo insuficiente para estudiar la corrección de argumentos como (1). En efecto, con el aparato formal que nos proporciona tampoco podemos dar cuenta de la validez de argumentos como (2) y (3).
(2) La ciudad de París es más grande que Madrid; por tanto, hay alguna ciudad que es más grande que Madrid.
(3) Si Cicerón es Tulio, entonces si Cicerón es calvo, Tulio es calvo.
La lógica de predicados, por el contrario, nos da herramientas formales para estudiar argumentos como (2) y (3), además de argumentos como (1). En primer lugar, si consideramos los argumentos (1), (2) y (3) observaremos los siguientes tipos de expresiones:
1. Nombres propios: «Madrid», «París», «Cicerón», «Piolín» y «Tulio». Con estas expresiones nos referimos a un objeto determinado.
2. Adjetivos y nombres comunes, con los que predicamos propiedades de los objetos: «calvo», «ave» y «alas».
3. Expresiones relacionales, con las que expresamos que un objeto está relacionado de determinada manera con otro. En nuestros ejemplos tenemos la expresión «es más grande que», que aparece en el argumento (2). La relación que aparece en (2) es binaria, porque relaciona dos individuos, sin embargo estas pueden ser ternarias, como por ejemplo, «b está entre a y c».
4. La relación de identidad, el «es» de (3). Es una relación especial.
5. Expresiones que nos ayudan a hablar de la totalidad de un dominio de objetos o de parte de él, como «todos», «hay» y «algunos». Estas expresiones se llaman cuantificadores.
6. Las conectivas que ya vimos cuando estudiamos el lenguaje de la lógica proposicional. Estas son expresiones veritativo-funcionales.
De este modo, como veremos en la próxima entrega de nuestro curso de lógica, la lógica de predicados incluye símbolos para expresar todas los tipos de expresiones de más arriba. De este modo, con la lógica de predicados podremos dar cuenta de argumentos cuya validez no depende únicamente de las conectivas, sino también del significado del resto de expresiones que hemos identificado en nuestra lista.
