Curso de lógica (V): semántica de la lógica proposicional: equivalencia lógica.

Vistas las tablas de verdad en la lección anterior de nuestro curso de lógica, pasaremos en esta lección a exponer el concepto de equivalencia lógica. Una vez expuesto este concepto, veremos cómo se puede utilizar para eliminar conectivas.

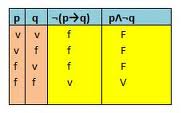
Dos fórmulas lógicamente equivalentes

La noción de equivalencia lógica

De forma intuitiva, si llevamos a cabo el procedimiento de las tablas de verdad y vemos que dos fórmulas tienen los mismos valores de verdad, para toda asignación, entonces diremos que esas fórmulas son lógicamente equivalentes. Para decirlo de manera formal, utilizaremos algunos signos del metalenguaje, que introducimos a continuación:

Utilizaremos el signo ν para referirnos a las asignaciones de valores de verdad, así ν(p) = V, significa que ν asigna a la letra p el valor verdadero».Y si le asignamos a p el valor falso, lo podemos expresar así: ν(p) = F.

Utilizaremos el signo ≡ para referirnos a la equivalencia lógica. Lo haremos así A ≡ B, significa que «A es lógicamente a B». Para negar la equivalencia lógica, utilizaremos este símbolo: /≡. A/≡B se lee «A no es lógicamente equivalente» o «A y B no son lógicamente equivalentes».

Y ahora expresamos la noción de equivalencia lógica formalmente:

A ≡ B si y solo si para toda asignación ν, ν(A) = ν(B).

Dada la tabla de verdad del bicondicional, «↔», es fácil confundirlo con la equivalencia lógica. Sin embargo debe tenerse en cuenta que el bicondicional es un símbolo del lenguaje de la lógica proposicional y que el símbolo de equivalencia lógica, «≡», pertenece al metalenguaje. En este caso, es un símbolo que introducimos en el castellano para expresar una relación entre fórmulas. Así, A ≡ B es un enunciado del castellano, mientras que A ↔ B es una fórmula del lenguaje de la lógica proposicional.

No obstante, la posible confusión del bicondicional con la equivalencia lógica tiene su base, puesto que A ≡ B si y solo si A ↔ B es una tautología. De este modo, podemos utilizar las tablas de verdad para averiguar si dos fórmulas son lógicamente equivalentes. Para saber si la fórmula A es equivalente a la fórmula B, basta con utilizar el procedimiento de las tablas de verdad para saber si la fórmula A ↔ B es una tautología.

La equivalencia lógica tiene tres propiedades básicas, evidentes por si mismas. Estas son las siguientes:

1. Toda fórmula es lógicamente equivalente a sí misma: A ≡ A (reflexividad).

2. Si A ≡ B, entonces B ≡ A (simetría).

3. Si A ≡ B y B ≡ C, entonces A ≡ C (transitividad).

Por último, respecto del concepto de equivalencia lógica, mostraremos una tabla de equivalencias lógicas famosas.

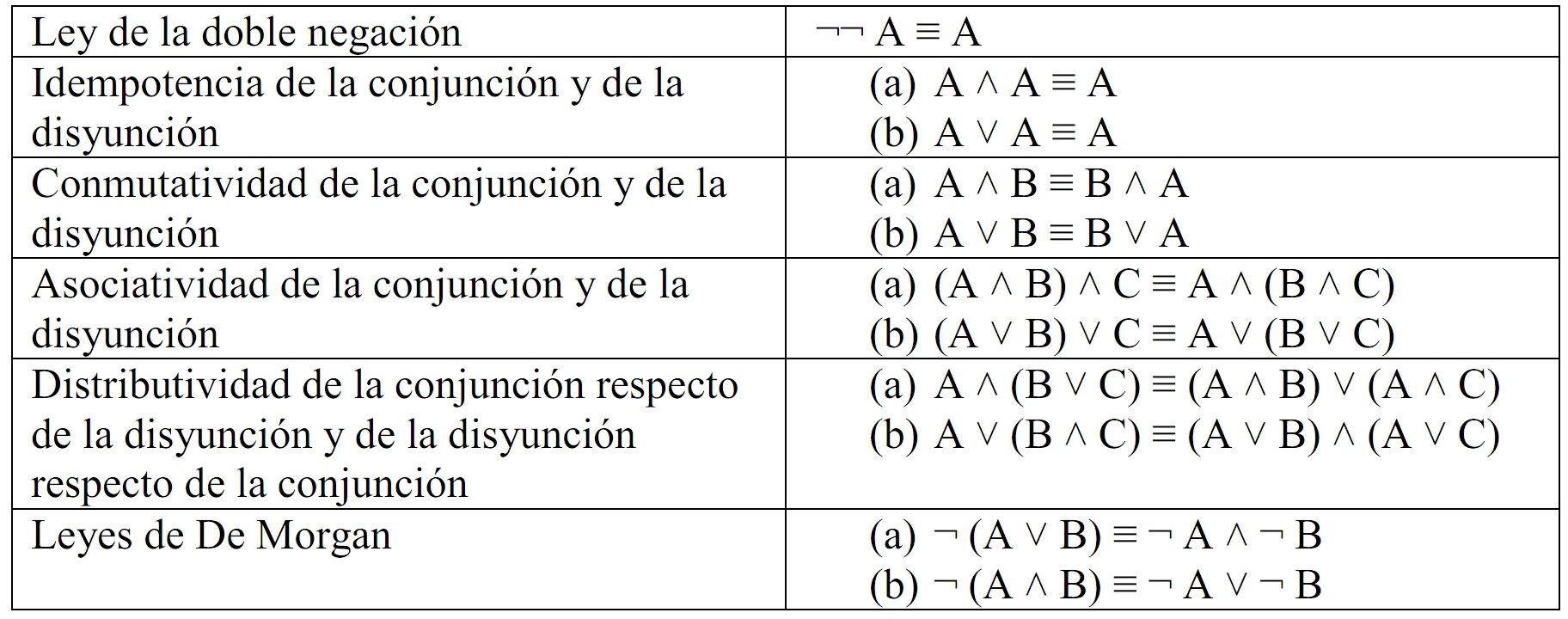
Eliminación de conectivas

Todas las conectivas de nuestro lenguaje proposicional se pueden eliminar, sustituyéndolas por otras, a excepción de la negación. Es decir, para cada conectiva, todo lo que se exprese con ella se puede expresar también utilizando otras conectivas. En la tabla de abajo se puede ver la lista de equivalencias entre las conectivas.

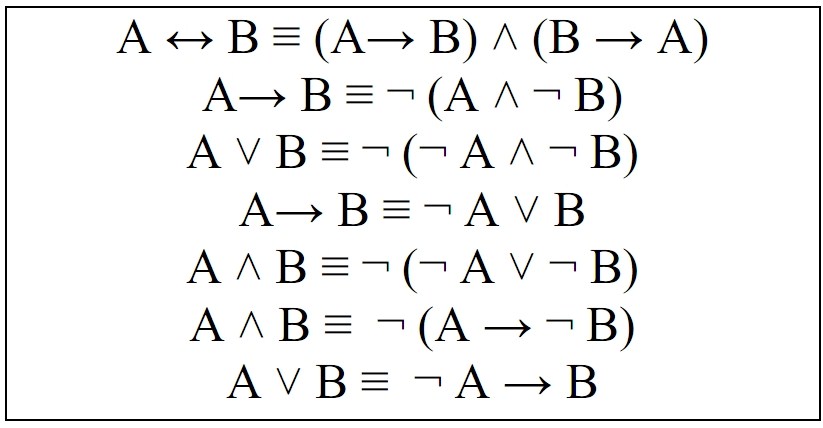
A continuación enumeraremos tres principios que nos ayudarán a eliminar conectivas.

Principio 1: Toda fórmula es lógicamente equivalente a una que tiene las mismas letras proposicionales y cuyas únicas conectivas son la conjunción y la negación.

Principio 2: Toda fórmula es lógicamente equivalente a una que tiene las mismas letras proposicionales y cuyas únicas conectivas son la disyunción y la negación.

Principio 3: Toda fórmula es lógicamente equivalente a una que tiene las mismas letras proposicionales y cuyas únicas conectivas son el condicional y la negación.

Esto implica que nuestro conjunto de conectivas, puede reducirse a dos. Según el primer principio, a la conjunción y la negación; según el segundo, a la disyunción y la negación y según el tercero, al condicional y la negación.

Bibliografía:

BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.