Curso de lógica (IV): Semántica de la lógica proposicional. Asignaciones y tablas de verdad
En las lecciones anteriores de nuestro curso de lógica hemos hablado de la sintaxis de la lógica proposicional. Ahora pasaremos a la semántica de la lógica proposicional. Para introducirnos en este campo, elucidaremos lo que es una asignación, para después pasar a explicar el método de las tablas de verdad.
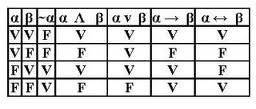
Tabla de verdad de las conectivas del lenguaje de la lógica proposicional
1. Asignaciones de valores de verdad
A cualquier letra proposicional de nuestro lenguaje le podemos asignar dos valores: el valor verdadero (en adelante V) y el valor falso (en adelante F). Estos se llaman valores de verdad. El número de asignaciones varía en función del número de letras proposicionales que tenga nuestro lenguaje. Un lenguaje con n letras proposicionales tendrá 2 elevado a n asignaciones de verdad.
En el caso de las fórmulas compuestas, su valor de verdad depende del valor de verdad de las letras proposicionales que las formas y del significado de las conectivas lógicas. En este caso se utilizan funciones veritativas. Se trata de funciones que asignan un valor de verdad a combinaciones de verdad, en función de la conectiva. Antes de continuar, introduciremos la noción de tabla de verdad.
2. Tablas de verdad
En función de los valores de verdad que nos dé una asignación de verdad para una fórmula dada, esta puede ser una contradicción, una tautología o una fórmula contingente. Si para toda asignación de verdad de una fórmula obtenemos que la fórmula es verdadera, entonces tendremos una tautología; si para toda asignación obtenemos una fórmula falsa, entonces estaremos ante una contradicción. Por último, si para toda asignación de verdad obtenemos que la fórmula es unas veces verdadera y otras falsa, entonces obtendremos una fórmula contingente.
Las tablas de verdad son un procedimiento que nos permite calcular el valor de verdad de una fórmula dada para cada asignación. Con el método de las tablas de verdad podemos decidir si una fórmula dada es una tautología, una contradicción o una fórmula contingente.
Dado todo lo dicho hasta ahora, a la hora de aplicar las tablas de verdad hemos de tener en cuenta las posibles asignaciones de verdad para cada letra proposicional de nuestro lenguaje (2 elevado a n), así como el significado de las conectivas. Respecto de lo primero ya hemos hablado. Pasemos a ver el significado de las conectivas en términos de valores de verdad, mediante una serie de reglas, cada una de las cuales rige sobre una de las conectivas de nuestro lenguaje:
Regla 1: Si el valor de verdad de p es V, entonces el valor de verdad de ̚ p es F y viceversa, si el valor de p es F, entonces el valor de ̚ p es V.
Regla 2: toda fórmula de la forma (p ˄ q) es verdadera si y solo si p es verdadera y q también lo es. Es falsa si p es falsa o q es falsa.
Regla 3: toda fórmula de la forma (p ˅ q) es verdadera si y solo si p es verdadera o q es verdadera. Si ambas subfórmulas son falsas, entonces la disyunción es falsa.
Regla 4: toda fórmula de la forma (p → q) es verdadera si y solo si el antecedente (p, en este caso) es falso o el consecuente (q) es verdadero. Es falso cuando el antecedente es verdadero y el consecuente es falso.
Regla 5: toda fórmula de la forma (p ↔ q) es verdadera si y solo si las subfórmulas que lo componen tienen los mismos valores de verdad y falso cuando sus subfórmulas tienen distintos valores de verdad.
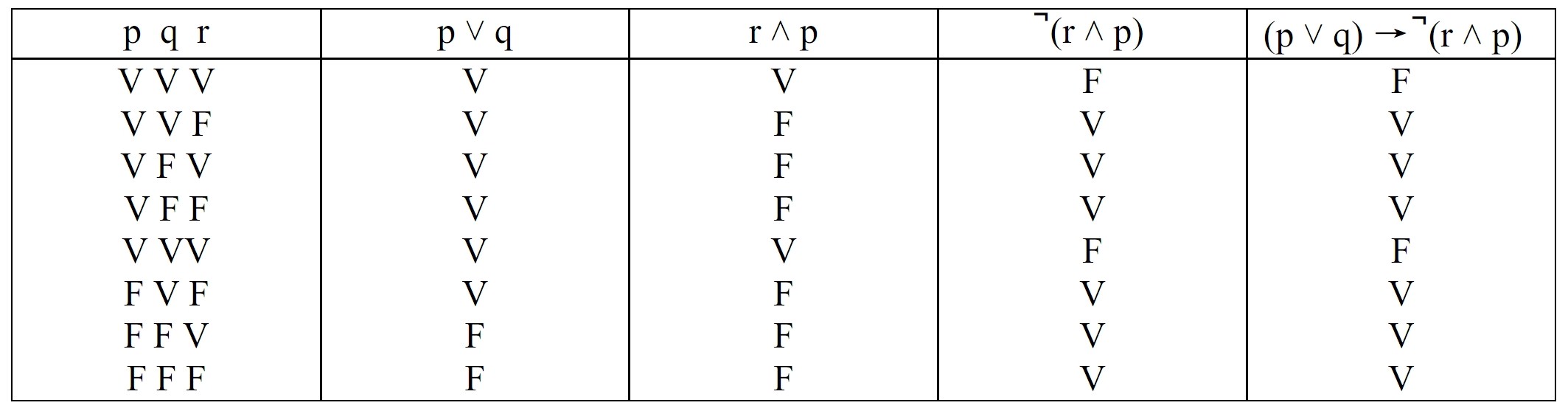
Para ver la aplicación de estas reglas y del procedimiento de las tablas de verdad, veremos la tabla de verdad de la fórmula (p ˅ q) → ̚ (r ˄ p)
Bibliografía:
BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.
