El principio del tercero excluido

El principio del tercero excluido es uno de los tres principios fundamentales de la lógica clásica, junto con los principios de identidad y de no contradicción, de los que hemos hablado aquí ya. Aparece en el análisis de los valores de verdad en el presente de los enunciados sobre el futuro realizado por Aristóteles en el De Interpretatione. Lo que este principio dice es lo siguiente:

(1) Todo enunciado es o verdadero o falso y no cabe otra posibilidad.

Este principio se formula en lógica proposicional así:

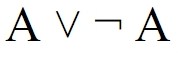
Principio del tercero excluido formulado en el lenguaje de la lógica proposicional

La lectura de la fórmula en el lenguaje natural es la siguiente: «A o no A». Se trata de una tautología. Este principio es exactamente el mismo que el principio de bivalencia, en el cual se basa la lógica clásica. Por ello, desde algunas de las lógicas no clásicas, como las lógicas trivalentes, el principio del tercero excluido no ha sido aceptado. De modo que a continuación veremos algunas de las críticas realizadas a este principio.

Las excepciones de Kant al principio del tercero excluido

Sin llegar a rechazarlo del todo, Inmanuel Kant pensó en algunas excepciones a este principio. En la Crítica de la razón pura, en la parte dedicada a las antinomias cosmológicas, el filósofo de Königsberg distingue dos tipos de antítesis: por un lado la analítica, en la que el principio del tercero excluido tiene plena validez; por otro lado estaría la oposición dialéctica, en la no tiene lugar este principio. Y pone un ejemplo para que quede claro. Este es, más o menos, como sigue.

(2) «El mundo es finito o infinito».

Si aceptamos la validez de la idea de mundo, entonces (2) será una oposición analítica y el principio del tercio excluido nos dice que (2) es evidentemente verdadera. Ahora bien, Kant piensa que la idea de mundo es algo que está más allá del alcance de nuestra intuición sensible, es un noúmeno y, por tanto, carece de validez, por lo que si se ve (2) como una oposición dialéctica, entonces hay que rechazarla ya que, para Kant, el mundo ni existe como un todo finito ni como un todo infinito.

Rechazo del principio del tercero excluido desde las lógicas no clásicas

Muchos lógicos vieron defectuosa la lógica clásica por diversas razones y algunos de estos propusieron lógicas trivalentes, es decir, lógicas en las que las fórmulas de aquellos lenguajes tuvieran tres valores de verdad y no dos. Esto por supuesto conlleva un rechazo del principio de bivalencia y del principio del tercero excluido.

Jan Łukasiewicz

Uno de los que criticaron la lógica bivalente sobre la base de importantes consideraciones filosóficas fue Jan Łukasiewicz, quien criticó la lógica bivalente llamando la atención sobre el hecho de que esta conllevaba el determinismo y el fatalismo. Łukasiewicz piensa que los sistemas lógicos bivalentes, como el de la lógica clásica, imponen unos esquemas deterministas en nuestro pensamiento, de modo que en el caso del valor de verdad que tienen en el presente los enunciados sobre el futuro, no deben ser considerados ni verdaderos ni falsos, sino «posibles» o «indeterminados». De este modo, el lógico polaco introdujo la primera lógica no clásica, el sistema Ł3. Este tenía dos conectivas primitivas (negación y condicional) y el cálculo de tablas de verdad del sistema se caracteriza por incluir un tercer valor.