Curso de lógica (XX): estructuras

Una vez hemos visto la sintaxis y la formalización al lenguaje de la la lógica de primer orden, vamos a pasar al ámbito del significado, de la interpretación de fórmulas y argumentos. La semántica de los lenguajes de primer orden se representa utilizando una estructura para ese lenguaje. Por su parte, una estructura para L es un par A = (U, F), donde U es un conjunto no vacío, el universo del discurso, formado por aquellos objetos sobre los que hablamos. Por su parte, F es una función cuyo dominio está formado por los símbolos propios de L y que cumple las siguientes condiciones:

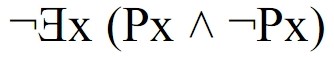
Interpretando los símbolos de un lenguaje para una estructura podemos determinar el valor de verdad de una sentencia de este tipo.

1. Si P es un símbolo de predicado de L, F(P) es un subconjunto de U.

2. Si S es un simbolo relacional n-ario de L (donde n > 1), F(R) es una relación n-aria en U.

3. Si c es una constante de L, F(c) es un elemento de U.

En resumidas cuentas, lo que estas tres condiciones vienen a decir es que dado un símbolo propio de L, s, F(s) es la interpretación de s en la estructura A. Fijar el significado de los símbolos propios de un lenguaje nos sirve para determinar el valor de verdad de una sentencia de ese lenguaje. Para hacer tal cosa necesitamos también echar mano del significado de las expresiones veritativo funcionales, esto es, de las conectivas. De este modo, una conjunción entre dos sentencias es verdadera en una estructura si y solo si cada una de ellas es verdadera; una disyunción de dos sentencias es verdadera si y solo si al menos una de ellas es verdadera; la negación de una sentencia es verdadera si y solo si la negación de esa sentencia es falsa; el condicional es verdadero si y solo si el antecendente es falso o el consecuente verdadero y el bicondicional es verdadero si y solo si ambas sentencias son falsas o ambas verdaderas. El cuantificador universal, por su parte, es verdadero si y solo si, dado un símbolo relacional o de predicado de L, en una fórmula de L con un cuantificador universal, todos los objetos del dominio de la estructura A pertenecen al conjunto con el que se interpreta a dicho símbolo de predicado o relacional de L. Del mismo modo, el cuantificador existencial es verdadero si y solo si hay algún objeto del dominio de la estructura A que pertenece al conjunto con el que se interpreta este hipotético símbolo de predicado o relacional.

Con un ejemplo. Supongamos que estamos hablando de los habitantes de la casa de La noche de los muertos vivientes (1968), de George A. Romero. Nuestro universo de discurso está formado por estos individuos, a los que nombramos con letras del alfabeto. Barbara, la chica catatónica, es a; Ben, el héroe afroamericano, es b; Karen Cooper, la niña herida, es c; Harry Cooper, el marido calvo, machista y dominante, es d; Hellen Cooper, la esposa del anterior, es e; Tom, el chico joven, es h y Judy, la chica joven, novia del anterior, es k. De este modo, U = {a,b,c,d,e,h,k} y ahora definamos los símbolos de L. Este cuenta con dos letras de predicado, P y Q, y un símbolo relacional, R. Asimismo, cuenta con siete constantes: a, b, c, d, e, h y k.

P es el conjunto de los habitantes que mueren devorados por los muertos vivientes.

Q es el conjunto de los habitantes que mueren por causas ajenas a los muertos vivientes.

R es una relación binaria discutir con entre individuos de la casa, de la forma (x,y) ϵ R si y solo si x discute con y.

a es Barbara

b es Ben

c es Karen Kooper

d es Harry Cooper

e es Hellen Cooper

h es Tom

k es Judy

Y ahora, en términos de nuestra estructura, vamos a determinar el valor de verdad de las siguientes sentencias:

¬Pb

∃xQx

∃xRxy ˄ ∀yQy

Veamos el valor de verdad de estas sentencias. Para todo el que haya visto la película, está claro que Ben, b, muere de un disparo en la cabeza, al ser confundido por un zombie, por tanto ¬Pb es verdadera, puesto que b no es un elemento de P, ya que P = {a,d,e}. Por su parte, ∃xQx es verdadera. En efecto, Q = {b,c,d}. Para quien no recuerde la película, Ben muere como ya hemos mencionado, en cuanto a Tom y Judy mueren cuando explota el depósito de gasolina. Finalmente, ∃xRxy ˄ ∀yQy es falsa. Por una parte, ∃xRxy es verdadera, pues R = {(b,d),(d,b),(d,e),(e,d)}. Sin embargo, ∀yQy es falsa, puesto que no todo miembro de U es miembro de Q, es decir, algunos habitantes de la casa mueren a causa de los muertos vivientes.

Bibliografía:

BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.