Curso de lógica (XVII): los lenguajes de primer orden

Tras haber dedicado un post introductorio a la lógica de predicados, vamos a pasar a caracterizar los lenguajes de primer orden. Todos ellos tienen en común los siguientes símbolos:

1. Variables: son infinitas. Para representarlas utilizaremos las letras «x», «y» y «z».

2. Conectivas: ¬, →, ↔, ˄, ˅.

3. Cuantificadores: el cuantificados existencial, ∃, y cuantificador universal, ∀.

4. Símbolo de identidad: =.

5. Paréntesis.

Los símbolos lógicos del lenguaje son los cuantificadores, las conectivas y el símbolo de identidad. Por su parte, los símbolos auxiliares son los paréntesis. Lo que distingue a cada lenguaje de primer orden de los demás son sus símbolos propios, los cuales pueden ser de tres tipos: símbolos de predicado, símbolos relacionales y constantes individuales. Con los primeros expresamos propiedades, con las segundas relaciones y las constantes individuales se comportan como nombres propios.

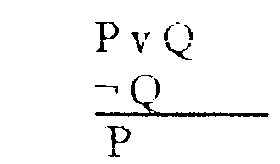
Como constantes de nuestro lenguaje de primer orden utilizaremos las letras «a», «b» y «c»; como símbolos de predicado utilizaremos las letras «P» y «Q». Por último, utilizaremos las letras «R», «S» y «T». Las relaciones pueden ser binarias, ternarias, …, n-arias.

Dado un lenguaje L de primer orden, una expresión de L es una sucesión finita de símbolos de L; un término de L es una variable o una constante de L.

Fórmulas

Sea L un lenguaje de primer orden con los siguientes símbolos {t, t», t»», P, R}, donde t, t», t»» son términos de L, P un símbolo de predicado de L y R un símbolo relacional n-ario de L, las fórmulas atómicas de L son las expresiones que tienen la siguiente forma: t = t», Pt, Rtt».

Una fórmula puede ser obtenida a partir de la aplicación del siguiente conjunto de reglas:

1. Toda fórmula atómica de L es una fórmula.

2. Si A es una fórmula (recordemos que utilizamos las letras A y B como variables de fórmulas), también lo es ¬A.

3. Si A y B son fórmulas, también lo son (A ˄ B), (A ˅ B), (A → B) y (A ↔ B).

4. Si A es una fórmula y x es una variable, ∀xA y ∃xA también son fórmulas.

El menor conjunto de expresiones de L que contiene todas las fórmulas de L y está cerrado respecto de 2-4 es el conjunto de las fórmulas de L. A partir de aquí obtenemos un principio de inducción para fórmulas: si L es un lenguaje de primer orden, P es una propiedad y

1. todas las fórmulas atómicas de L tienen la propiedad P,

2. si A es una de L con la propiedad P, ¬A también tiene la propiedad P,

3. si A y B son fórmulas de L con la propiedad P, las fórmulas (A ˄ B), (A ˅ B), (A → B) y (A ↔ B) también tienen la propiedad P,

4. si A es una fórmula de L con la propiedad P y x es una variable, las fórmulas ∀xA y ∃xA también tienen la propiedad P,

entonces toda fórmula de L tiene la propiedad P.

Estas expresiones son fórmulas no atómicas: ¬ x = y, ¬Qx, Qx → Ryx, ∀xQx, ∀x¬Qx, ∀x∀y (Qx → Sxy)…

Subfórmulas

Del mismo modo que hacíamos en lógica proposicional, podemos describir la generación de una fórmula dada, de acuerdo con las reglas que hemos dado anteriormente, asociándole su árbol genealógico. Así, por ejemplo, la fórmula ∀x∃y(Qx ˄ Sxy) → ¬Saa se descompone de la siguiente manera:

Nivel 1: ∀x∃y(Qx ˄ Sxy), nivel 1″: ¬Saa

Nivel 2: ∃y(Qx ˄ Sxy), nivel 2″: Saa

Nivel 3: (Qx ˄ Sxy), nivel 3″: –

Nivel 4: Qx, Sxy, nivel 4″: –

Bibliografía:

BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.