Curso de lógica (XVIII): variables

Nuestro curso de lógica avanza al mismo ritmo al que avanza la miseria en España, así que nos vemos ya en el tema de las variables, un paso imprescindible en el que nos tenemos que parar para hacer frente más adelante a los modelos y al cálculo deductivo.

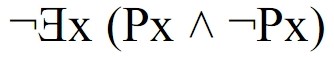
En este caso, x es una variable ligada a un cuantificador existencial

Variables libres y variables ligadas

A las expresiones de la forma ∀x y ∃x las llamaremos expresiones cuantificadas. Son expresiones formadas por un cuantificador seguido por una variable. Pues bien, en una fórmula un mismo símbolo puede aparecer varias veces, pudiendo presentar distintas apariciones. Y esto se aplica también a las variables. En el caso de estas, pueden aparecer como variables libres o variables ligadas.

Una variable es ligada cuando dada una fórmula en la que tal variable aparece, esta forma parte de una subfórmula del tipo ∀xB o ∃xB. En este caso, decimos que x es una variable ligada por el cuantificador universal o existencial, respectivemente. Y, al contrario, cuando la aparición de una variable en una fórmula no es ligada, decimos que es una variable libre. Vamos a poner un par de ejemplos de variables libres y ligadas:

∀x(Qx ˄ Rxy), en esta fórmula la x es una variable ligada por un cuantificador universal, tanto en Qx como en Rxy, y la variable y es libre.

∀x(Qx ˄ Rxy) → (∃yQy → Rxz), en esta fórmula, la primera aparición de x, en Qx y en Rxy, es ligada por un cuantificador universal. Por su parte, la segunda aparición de x, en Rxz, es libre. En cuanto a y, en su primera aparición es libre, mientras que en la segunda, ∃yQy, aparece ligada por un cuantificador existencial. Por último, z aparece una sola vez y es libre.

A las fórmulas con una o más variables libres las llamamos fórmulas abiertas, mientras que a las fórmulas sin variables libres las llamamos fórmulas cerradas o sentencias. Estas se corresponden con enunciados del lenguaje natural y cuando se las interpreta tiene sentido preguntarse si son verdaderas o falsas. Las siguientes son fórmulas cerradas:

a = b

∀x(Px ˄ Qx)

Pc → Rac

∀x∃y(Sxy ˄ ¬Syx)

Y las siguientes fórmulas son ejemplos de fórmulas abiertas:

a = x

∀x(Px ˄ Qy)

Pz

∀x∃y(Sxy ˄ ¬Syx) ˅ (Px ↔ Sxy)

Sustitución de variables

Las fórmulas abiertas pueden transformarse en sentencias sustituyendo las variables libres por términos. Al hacer tal sustitución obtenemos una nueva fórmula. De este modo, si en una fórmula, A, aparece libre la variable y, si sustituimos y por un término, t, obtenemos la sustitución de y por t, que expresamos formalmente así A(y/t). Así,

1. Py(y/c) su sustitución es la fórmula Pc

2. Qx ˄ ∀x(Px → ∃yQy)(x/a) su sustitución es la fórmula Qa ˄ ∀x(Px → ∃yQy)

3. Rxy ↔ Ryx(y/c) su sustitución es la fórmula Rxc ↔ Rcx

4. ∀x(Px ˄ Qy)(x/a) su sustitución es la fórmula ∀x(Px ˄ Qy)

5. Py(x/c) su sustitución es la fórmula Py

En los ejemplos 4 y 5 no hay que reemplazar símbolo alguno, puesto que en ningún caso la variable a sustituir aparece libre en estas fórmulas. En cuanto al ejemplo 2, solo se reemplaza la x en la primera aparición, Qx, que es en la única en la que aparece libre.

Bibliografía:

BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.