Wittgenstein VI: las proposiciones II
Como dijimos en la primera entrada dedicada a la concepción de las proposiciones de Wittgenstein, íbamos a dedicar aquella a las proposiciones de la ciencia natural, dejando las proposiciones de la lógica para una entrada posterior. Pues bien, de estas hablaremos aquí, partiendo de lo dicho en el post anterior a este, dedicado a la teoría de la negación de Wittgenstein.

Caricatura de Ludwig Wittgenstein
Las proposiciones de la lógica y la concepción figurativa del lenguaje
Según la teoría de la negación de Wittgenstein, captar el sentido de una proposición es captar las circunstancias que la harían verdadera, lo que supone captar las circunstancias que la harían falsa. Ahora bien, las proposiciones de la lógica son necesarias, esto es, verdaderas independientemente de las circunstancias. Esto lleva a una tensión: según el punto de vista de Wittgenstein, las proposiciones no pueden ser verdaderas cualesquiera sean las circunstancias. ¿Cómo resuelve esta aparente incongruencia?
Las tablas de verdad
Aunque Wittgenstein nunca dio un ejemplo de proposición elemental, estas juegan un papel destacado en su teoría. Para empezar, los nombres propios del lenguaje ordinario, «París» o «Sócrates», por ejemplo, son en realidad estructuras complejas formadas por estas proposiciones elementales. A su vez, estas proposiciones elementales se combinan para formar proposiciones complejas.
Sin embargo, Wittgensteín sí que señaló cómo se relacionan las proposiciones elementales con las complejas: una proposición compleja es una función de verdad de proposiciones elementales. ¿Qué quiere esto decir? Pues que el valor de verdad que puede tomar una proposición compleja depende de los posibles valores de verdad que pueden tomar las proposiciones simples.
Supongamos que tenemos una proposición compleja, «p y q». Esta está formada por dos proposiciones simples, «p» y «q», las cuales están combinadas de determinada manera, mediante el signo «y», una constante lógica.
Bien, es posible que «p» sea verdadera y «q» también lo sea, en cuyo caso, «p y q» será verdadera. Asimismo, es posible que ambas sean falsas, por lo que «p y q» será falsa. Puede ser que «p» sea falsa y «q» verdadera, o viceversa, «p» verdadera y «q» falsa. En ambos casos, «p y q» es falsa. (Ver la entrada dedicada a las tablas de verdad de nuestro curso de lógica).
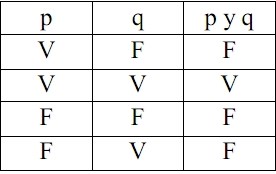
Esta es la tabla de verdad de «p y q» y es equivalente a la misma proposición, esto es, lo mismo daría poner «p y q» que «FVFF(p,q)». Ahora bien, la tabla muestra que el sentido de «p y q» es equivalente a sus condiciones de verdad. Y, lo que es más, muestran que las constantes lógicas, «y» en este caso, no están por objetos, pues en realidad también son equivalentes a las condiciones de verdad de las proposiciones complejas.
Pues bien, Wittgenstein llama la atención sobre dos tipos de proposiciones que se pueden construir sobre esta base, unas que son verdaderas para todas las posibilidades de verdad de las proposiciones elementales que las componen, y otras que son falsas para todas las posibilidades de verdad de sus proposiciones elementales. Son las tautologías y las contradicciones, respectivamente.
Por ejemplo, «p y no-p» es una contradicción, como muestra su tabla de verdad:
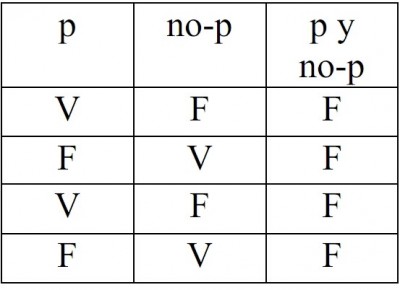
Y «si p, entonces p» es una tautología:

Ahora bien, tal y como dice Wittgenstein en el Tractatus, en 4.4611, ni las contradicciones ni las tautologías tienen sentido. Por ejemplo, si digo «un huevo, es un huevo», no estoy figurando nada, esa proposición no me informa de nada, por más que sea verdadera independientemente de cuáles sean las circunstancias. Esto quiere decir que no dice nada. Pero entonces, ¿cómo pueden ser proposiciones? Muy sencillo (bueno, no tanto), porque aunque carezcan de sentido y no digan nada, tampoco son sinsentidos, es decir, no son galimatías como «tururú».
Tanto las tautologías como las contradicciones forman parte del simbolismo. Las tablas de verdad de las tautologías y las contradicciones siguen las mismas reglas que las tablas de verdad de las proposiciones figurativas. Los sinsentidos o galimatías, como «potrotranco estrambótico jacinporleado» no siguen ese tipo de reglas. Ahora bien, aunque las contradicciones y tautologías sean mudas en este sentido, no digan nada, sí que muestran algo sobre la lógica. Por ejemplo, «p y no p» muestra que esta combinación no dice nada, pero como no dice nada, no lo puede decir, ya que si dijera que no dice nada, estaría diciendo algo, por eso lo muestra.
En la medida en que contradicciones y tautologías nos revelan la naturaleza de la lógica, conocemos las reglas que reflejan la forma lógica, gracias a las cuales podemos construir proposiciones con sentido, esto es, que digan algo.
Las proposiciones de la lógica son tautologías
Desde este punto de vista, para Wittgenstein las proposiciones de la lógica son tautologías. Estas muestran la forma lógica, pero no dicen nada. Además, para Wittgenstein todas las proposiciones están a un mismo nivel. Los sistemas lógicos de Frege y Russell establecían una jerarquía entre proposiciones: por un lado estaban los axiomas y por otro las proposiciones extraídas de estos (teoremas). Estos eran extraídos mediante unas leyes de inferencia, del tipo «si tienes «si p, entonces q» y «p», puedes inferir (o deducir o derivar) «q»».
Sin embargo, esto planteaba una serie de problemas. En primer lugar, cómo la verdad de los axiomas se mantiene en las proposiones que se derivan de ellos o en qué sentido los axiomas son más fundamentales que las verdades lógicas que se derivan de ellos. Asimismo, el status de las leyes de inferencia tampoco queda claro, no se sabe, por ejemplo, si se basan en alguna verdad lógica ni si está es más fundamental que los axiomas.
Wittgenstein presentó una noción de inferencia que disolvía estos problemas. Para él ninguna proposición es más fundamental que otra, y los axiomas que elijamos es una cuestión arbitraria. Según su punto de vista, la inferencia se apoya en la estructura interna de la proposición. En efecto, lo que muestran las tablas de verdad es que el sentido de unas proposiciones está contenido en el sentido de otras, que los fundamentos de la verdad de una están contenidos en otras. Por ejemplo, decir que «p» se sigue de «p y q» no es más que decir que el sentido de «p» está en «p y q» o que la verdad de «p» está contenida en «p y q».
Las proposiciones derivadas de los axiomas son un desarrollo de estos que se limitan a aclarar su contenido. Los sistemas lógicos no tratan sobre la realidad, sino sobre sí mismos, muestran cómo se relacionan los sentidos de las proposiciones entre sí. Así, desde el punto de vista de Wittgenstein, las leyes de la inferencia de Frege y Russell están de más. Y los axiomas tienen dicho estatus por una decisión arbitraria. En realidad, «p y q» podría ser un axioma respecto de «p», en la misma medida en que «p» podría serlo con respecto a «p y q».
Pues bien, estas tautologías son las proposiciones de la lógica, la lógica es así un sistema de tautologías que no dice nada, pero que muestra la forma lógica. En el caso de Wittgenstein, la tarea de los sistemas lógicos consiste en exhibir o mostrar la lógica del lenguaje ordinario de un modo más claro y perspicuo de lo que el lenguaje ordinario podría hacerlo.
