Tautología

En lógica, se le llama tautología a toda fórmula que es verdadera para toda asignación de valores de verdad. De un modo más formal, podemos definir una tautología como sigue: la fórmula A es una tautología si y solo si para toda asignación v, v(A) = V. En lógica proposicional, podemos reconocer una tautología mediante el procedimiento de las tablas de verdad. Las tautologías tienen siempre en su columna final el valor verdadero, independientemente de los valores de verdad que aparece en las columnas de sus subfórmulas. Estos son la definición de tautología y un procedimiento para reconocer tautologías y a muchos no les dirán gran cosa. Así que voy a poner algunos ejemplos informales de tautologías:

(1) lo que es, es.

(2) Lo haces o no lo haces.

Las formas lógicas de (1) y (2) serían

(1″) p = p

(2″) q ∨ ¬q

A primera vista, las tautologías son bastante triviales, sobre todo cuando las consideramos tomando como punto de referencia el lenguaje natural. Y, es cierto, en ocasiones lo son. Pero si en ocasiones las expresiones del lenguaje natural cuya forma lógica es tautológica son triviales, entonces, también en ocasiones no lo son.

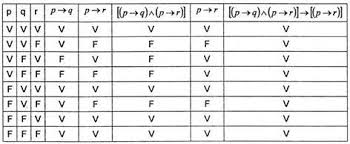
Tabla de verdad de una tautología.

Decir cosas no triviales con expresiones tautológicas

El segundo Wittgenstein decía en las Investigaciones filosóficas que el lenguaje natural que era más complejo y cambiante de lo que los filósofos del lenguaje habían creído, incluido él mismo. Hoy en día sospecho que muy poca gente discute esto. Y este es el caso con expresiones cuya forma lógica es tautológica: que decimos muchas cosas con ellas e, incluso, somos capaces de explotar su fórmula lógica para decir más cosas o hacer chistes.

Obviamente, a esta conclusión no he llegado reflexionando sobre la naturaleza del lenguaje, sentado en el sofá de mi casa. Más bien, estaba bebiendo cerveza con un amigo, el cual me estaba hablando sobre su trabajo como peón agrícola en la recolección de la aceituna. En el transcurso de la conversación profirió la siguiente expresión tautológica:

(3) «yo, cuando voy a trabajar, voy a trabajar»

Cuya forma lógica es

(3″) p → p

Tomada (3) aisladamente, tal y como aquí la estoy presentando, es una trivialidad. Sin embargo, en el contexto en el que fue utilizada significaba lo que podemos expresar con el siguiente enunciado:

(4) yo, cuando voy a trabajar, rindo sobradamente.

Sé (y podemos saber) que (3) significa lo enunciado en (4) porque el contraste realizado por mi amigo, el hablante, era con ejemplos de otras personas que iban al trabajo y no rendían. Por mi parte, cuando yo oí (3), le dije, de forma jocosa, al captar su forma tautológica, algo así: «o sea, que tú, cuando vas a trabajar, vas a trabajar». A lo que él respondió, de forma irónica: «no, voy a echar el trompo» («trompo» significa en el lenguaje de Baena – Córdoba, España – «peonza»). En mi opinión, su respuesta irónica era una manifestación de su conocimiento de que (3) es, en cierto modo, trivial (por tautológica). De modo que este hablante, hasta cierto punto muy parecido a cualquier otro, no solo utilizaba (3) para decir algo no trivial, sino que captó que tenía la forma de una tautología. Obviamente, él ni sabe qué es una tautología ni qué es su forma lógica, pero captó la lógica de la expresión.