La paradoja del mentiroso

La paradoja del mentiroso está entre los rompecabezas más complicados que han ocupado las cabezas de los filósofos más sesudos desde la antigüedad. Esta cuenta con diversas variantes, muchas de ellas pensadas para superar los intentos de solución que se han planteado en la historia de la filosofía. El interés de la paradoja del mentiroso es tal, que una teoría de la verdad que no se enfrente a ella carece de interés.

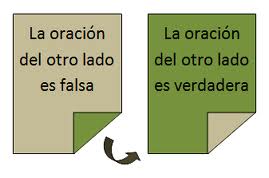
Tercera versión de la paradoja del mentiroso

1. Algunas variantes de la paradoja del mentiroso

La versión clásica de la paradoja del mentiroso se puede expresar en la oración (1)

(1) Esta oración es falsa.

Si suponemos que (1) es verdadera, entonces que (1) es falsa es el caso y, por tanto, (1) es falsa. Pero esto va en contra de nuestra suposición inicial, a saber, que (1) es verdadera. Supongamos ahora que (1) es falsa. Si (1) es falsa, entonces (1) no es el caso, y por tanto es verdadera, es decir, si es falso que «esta oración es falsa», entonces será verdadera.

Otra versión de esta paradoja, la tenemos en (2)

(2) La siguiente oración es falsa. La anterior oración es verdadera.

Si la primera oración de (2) es verdadera, entonces la siguiente es falsa y, por tanto, la primera

oración es falsa, lo que va en contra de nuestra suposición inicial. Ahora bien, supongamos que la primera oración de (2) es falsa, entonces la siguiente es verdadera y, por tanto, la primera oración es verdadera, lo que, nuevamente, va en contra de la suposición inicial. Muy similar a esta variante es la siguiente: en una de las caras de un folio escribimos (3)

(3) la oración escrita en la otra cara de este folio es falsa.

Y (4) en la otra cara,

(4) la oración escrita en la otra cara de este folio es verdadera.

De nuevo, si (3) es verdadera, entonces (4) es falsa y, por tanto, (3) será falsa. Algo que, nuevamente, va en contra de nuestra suposición inicial. Ahora bien, supongamos que (3) es falsa. Si (3) es falsa, entonces (4) es verdadera y, por tanto, (3) es verdadera. Una vez más, contradecimos nuestra suposición inicial.

2. Algunas posibles soluciones a la paradoja del mentiroso

Como decíamos al principio, la paradoja del mentiroso ha estimulado a las mentes más preclaras de la historia del pensamiento. No obstante, a pesar de la diversidad de soluciones, aquí expondremos solo dos de ellas, la de Alfred Tarski y la de Saul A. Kripke.

Alfred Tarski da una solución formal a la paradoja del mentiroso. En su opinión la paradoja del mentiroso se debe a aceptar la suposición de que el lenguaje es semánticamente cerrado. Suponer esto es equivalente a suponer que contiene dos elementos: 1) medios para referirse a sus propias expresiones y 2) los predicados «verdadero y falso».

Su solución es dar una definición de verdad para los lenguajes semánticamente abiertos. Para entender esta noción hay que partir de una jerarquía de lenguajes, la cual contiene los siguientes:

(L) El lenguaje objeto.

(M) El metalenguaje. Este contiene los medios para referirse a expresiones de L y los predicados «es verdadero en L» y «es falso en L».

(M») El metametalenguaje, que contendría los medios para referirse a expresiones de M y los predicados «es verdadero en M» y «es falso en M».

Y así sucesivamente.

La solución de Tarski convierte la paradoja del mentiroso en una oración falsa. Por ejemplo, (1) se reformularía como (1″)

(1″) Esta oración es falsa en L.

Ahora bien, (1″) no es una oración de L, sino de M.

La solución de Saul Kripke es bien distinta. Desde su punto de vista, más que una jerarquía de lenguajes, habría una jerarquía de niveles del lenguaje. Parte de cómo se le explicaría el concepto de verdad a alguien que no lo entiende. Según Kripke, le explicaríamos que puede decir que una oración es verdadera, cuando puede aseverarla fundamentadamente y puede decir que no es verdadera cuando puede negarla fundamentadamente. La noción de fundamentación es esencial. Por ejemplo, si el aprendiz está fundamentado para decir (5)

(5) La nieve es blanca.

Puede entonces decir (6)

(6) La nieve es blanca es verdadera.

A partir de aquí, el aprendiz puede extender el uso de «es verdadero» a otras oraciones. Es decir, se puede predicar el predicado «es verdadero» cuando la oración está fundamentada. ¿Qué ocurre con la paradoja del mentiroso? Según Kripke (1) no está fundamentada y, por tanto, no es una oración verdadera ni falsa. La ventaja de Kripke es que no asume que toda oración es, de forma unívoca, o bien verdadera o bien falsa. Es decir, para Kripke hay dos valores de verdad: verdadero y falso. Y también hay oraciones que no tienen valor de verdad, como (1).

Bibliografía

Haack, S.: Filosofía de las lógicas, Cátedra, 1982. Madrid

Imagen: nosaber.com