Gottlob Frege II: análisis lógico en términos de argumento y función
En 1874 Gottlob Frege consiguió una plaza de Privatdozent en la Universidad de Jena. Ese mismo año comenzaría a trabajar en una de sus obras más fundamentales: la Conceptografía (en alemán, Begriffsschrift). En esta obra Frege sembró los fundamentos de la lógica actual, suponiendo la mayor transformación que esta ciencia ha experimentado desde la época de Aristóteles.
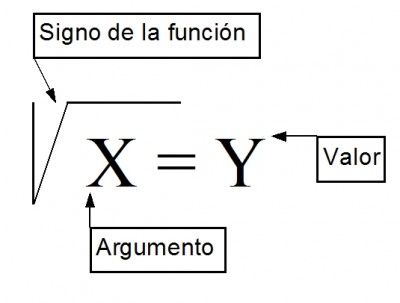
Frege se inspiró en las funciones matemáticas para diseñar su análisis lógico en términos de argumento y función
Inferencias y contenido conceptual
La Conceptografía es un lenguaje simbólico, que emula al de la aritmética. De hecho, se trata de una especie de instrumento de precisión, diseñado para examinar las relaciones inferenciales entre las proposiciones. Con ello pretendía Frege dotar a la aritmética, a la base de las ciencias, de unos fundamentos seguros. Se trataba de los fundamentos lógicos de las inferencias en aritmética. Con esto Frege se propuso la meta de reducir toda la aritmética a la lógica. Su objetivo era probar el logicismo.
El lenguaje de fórmulas de Frege estaba ideado para poner de manifiesto el contenido conceptual de las oraciones. Este es el soporte que nos permite pasar de unas proposiciones a otras siguiendo reglas lógicas de derivación. Esto son las inferencias, lo que Frege quería estudiar. Ahora bien, Frege pensaba que el lenguaje ordinario no podía garantizar la seguridad epistemológica que requería la ciencia, pues frecuentemente daba lugar a ambigüedades y vaguedades. Por ello ideó esta herramienta de precisión.
Para Frege el lenguaje ordinario era mucho más versátil que su conceptografía. Esta era una herramienta de precisión para realizar una tarea muy específica y particular: examinar las relaciones inferenciales para comprobar si están lógicamente justificadas. Ahora bien, su conceptografía era completamente inútil para realizar cualquier otra cosa. La relación entre el lenguaje simbólico de fórmulas de Frege y el lenguaje ordinario es análoga, según el mismo Frege explica, a la existente entre el ojo humano y el microscopio: el primero es muy versátil y útil para infinidad de situaciones; mientras que el segundo es una herramienta de precisión, mejor que el ojo para llevar a cabo la tarea para la que ha sido diseñado, pero inútil para realizar cualquier otra cosa.
Lógica y gramática
Uno de los grandes aportes de Frege fue separar entre el análisis lógico de las oraciones y el análisis gramatical de estas, los cuales completamente distintos. Para verlo utilizaremos un ejemplo del propio Frege.
(1) Los griegos derrotaron a los persas
(2) Los persas fueron derrotados por los griegos
Desde un punto de vista gramatical las diferencias entre (1) y (2) son palpables. Por ejemplo, el sujeto de (1) es «Los griegos», mientras que el de (2) es «Los persas». De hecho, también existe una diferencia desde un punto de vista estilístico. Ahora bien, desde un punto de vista lógico, (1) y (2) son equipolentes, esto es, cualquier cosa que se siga lógicamente de (1), se sigue también de (2), y viceversa. Así que (1) y (2) tienen el mismo contenido conceptual, aunque sean gramatical y estilísticamente distintas.
Análisis en términos de argumento y función
La lógica tradicional había asumido, desde la época de Aristóteles, el análisis de las oraciones en términos gramaticales, esto es, sustentándolo en las categorías de sujeto y predicado. Tales categorías tenían el problema, a ojos de Frege, de que no tenían en consideración el contenido conceptual de las oraciones. Por ello Frege propuso un análisis lógico sustentado en dos categorías extraídas de la matemática: argumento y función.
Para ver cómo funciona este tipo de análisis, añadiremos la oración (3)
(3) Los griegos derrotaron a los partos
(1) y (3) tienen diferente contenido conceptual y esto puede reflejarse mediante el análisis de Frege. Según este, tanto (1) como (3) cuentan con una parte constante y otra variable. Frege llama a la primera función y a la segunda argumento. En (1) y (3) la función es «los griegos derrotaron a…» y los argumentos son «los persas» y «los partos», respectivamente. A su vez, (1) es el valor de la función «los griegos derrotaron a…» para el argumento «los persas» y (3) es el valor de esta función para el argumento «los partos».
(1) y (3) también permiten un análisis equivalente, en los mismos términos. Así, podemos considerar que la función es «…derrotaron a…», en (1) la función está saturada por el par de argumentos (los griegos, los persas) y en (3) con el par (los griegos, los partos). Y, del mismo modo que en el caso anterior, (1) es el valor de la función «…derrotaron a…» para el par de argumentos (los griegos, los persas) y (3) es el valor de esta función para el par (los griegos, los partos).
Sea como fuere, lo que esto pone de manifiesto es que el análisis lógico nos permite, además, distinguir las funciones según se saturen con un solo argumento (propiedades) o con dos (relaciones).
Generalidad lógica
Uno de los grandes aportes de Frege a la lógica y que explica la importancia de la distinción entre argumento y función, fue su tratamiento de la generalidad, es decir, de oraciones como (4)
(4) Todo humano es mortal
En (4) distinguimos la función «todo humano es…» y el argumento «mortal». Ahora bien, pensemos en (5)
(5) Juan es mortal
En (5) tenemos la función «…es mortal» saturada con el argumento «Juan». ¿Qué diferencia hay entre las funciones «todo humano es…» y «…es mortal»? La primera es una función de segundo orden y la segunda es de primer orden. Esto quiere decir que la segunda se satura con argumentos como «Juan» que, por sí mismos, representan una idea independiente. Por su parte, las funciones de segundo orden tienen como argumentos funciones de primer orden.
