Curso de lógica (XV). Teoría de conjuntos (IX): funciones
En las dos anteriores entradas de nuestro curso de lógica dedicadas a las relaciones dejamos sentadas las bases para pasar a ver las funciones. Una vez vistas estas daremos por terminado el grupo de entradas del curso de lógica dedicadas a la teoría de conjuntos. Con todo esto tendremos las nociones suficientes para pasar a ver la lógica de predicados de primer y segundo orden. De este modo pasamos ya a ver las funciones sin más dilación.
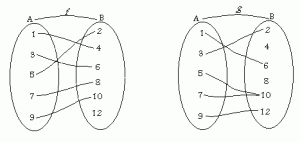
¿Qué es una función?
Una función es un tipo específico de relación. En una función unas cosas se relacionan con otras de un modo tal que ningún objeto se relaciona a la vez con más de un objeto. De este modo estamos ante funciones cuando asignamos a este blog su número de entradas en un momento dado, cuando identificamos personas haciendo referencia a otras («la madre de Fulanito, por ejemplo»), cuando determinamos el peso de un perro, etc. Como se puede observar si se piensa en estos ejemplos se verá que el número de entradas de este blog en un momento dado es único, al igual que la madre de Fulanito o el peso de un perro. Para definir una función con mayor rigor podemos decirlo así: una función es una relación R tal que para cualesquiera objetos a,b,c, si (a,b) ϵ R y (a,c) ϵ R, entonces b = c. O lo que es lo mismo: dada una relación R, esta es una función si y solo si para todo a ϵ dom(R) hay un único objeto b tal que (a,b) ϵ R.
Para referirnos a funciones utilizaremos las letras «f», «g» y «h». Estas letras serán nuestras variables de funciones.
El valor de una función
Dada una función f, si a ϵ dom(f), f(a) es el único objeto b tal que (a,b) ϵ f. De este modo, para todo a ϵ dom(f), f(a) = b si y solo si (a,b) ϵ f. Pues bien, en este caso f(a) es el valor que f asigna al argumento a. «Argumento» significa aquí «elemento del dominio».
Dado un objeto b, este es un valor de la función f si y solo si hay un objeto a ϵ dom(f) tal que f(a) = b o, lo que es lo mismo, (a,b) ϵ f. De este modo, b es el valor de f si y solo si b ϵ rec(f) y esto significa que rec(f) es el conjunto de los valores de f. Así, rec(f) = {f(x) : x ϵ dom(f)}.
Como hemos dicho al principio, las funciones son un tipo particular de relaciones y, como tales, son conjuntos de pares ordenados. Ahora bien, eso significa que se rigen por los mismos principios por los que se rigen el resto de conjuntos. De este modo, las funciones cumplen el principio de extensionalidad, son extensionales. De este modo, f = g si tienen los mismos elementos. O dicho con mayor precisión: f = g si y solo si dom(f) = dom(g) y si para todo par (a,b), (a,b) ϵ f si y solo si a ϵ dom(f) y f(a) = b y (a,b) ϵ g si y solo si a ϵ dom(g) y g(a) = b.
Bibliografía:
BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.
