Curso de lógica (VII): Teoría de conjuntos (I): ¿Qué es un conjunto?
Vista la lógica proposicional en los capítulos II-VI de este curso de lógica, pasamos a continuación a la teoría de conjuntos, la cual nos será muy útil para el estudio de la lógica de predicados de primer y segundo orden. Esta primera lección la dedicaremos a esclarecer la noción de conjuntos, así como algunas otras nociones que utilizaremos.
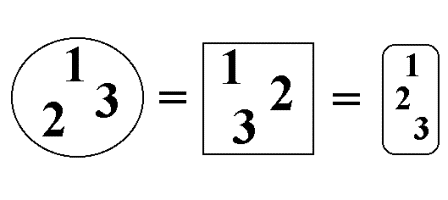
Los tres conjuntos son el mismo en virtud del principio de extensionalidad.
Un conjunto es una colección de objetos. A estos objetos los llamamos elementos del conjunto. Cada objeto dado puede ser elemento de un conjunto. De este modo, una palabra, un elefante, un número, un país o un conjunto pueden ser elementos de un conjunto. Por supuesto, los conjuntos son objetos y pueden ser elementos de un conjunto, esto es, hay conjuntos de conjuntos. Bien, dado un objeto x y un conjunto A, podemos expresar que «x es un elemento de A» o que «x pertenece a A», mediante la siguiente fórmula: «x ϵ A». Para decir que «x no es un elemento de A» o que «x no pertenece a A» utilizaremos la fórmula siguiente: «x ϵ/ A».
Para indicar que dos objetos cualesquiera, x e y, son el mismo objeto utilizaremos la fórmula «x = y». Para expresar que son objetos distintos utilizaremos la fórmula: «x ≠ y». Los objetos estarán clasificados en dos categorías: objetos primitivos, que son aquellos objetos que no tienen elementos, y conjuntos, que son aquellos objetos con elementos. Para referirnos a conjuntos utilizaremos letras latinas en mayúscula: A, B, C, etc. Para objetos, utilizaremos letras latinas minúsculas: a, b, c… Las letras mayúsculas son variables de conjuntos, las minúsculas de objetos.
Según el principio de extensionalidad, si un conjunto A y un conjunto B tienen exactamente los mismos elementos y ninguno más, entonces A = B. Dicho de otro modo, si todo elemento de A pertenece a B y todo elemento de B pertenece a A, entonces A = B. De aquí se sigue que lo que define en última instancia a los conjuntos son los elementos que lo forman.
Por último, dedicaremos en este capítulo para hablar sobre el modo en el que nos referiremos a los conjuntos. Los conjuntos son objetos abstractos y, como tales, no están ni en el espacio ni en el tiempo. No son objetos que se puedan señalar, sin embargo, sí que los podemos nombrar. Esto lo podemos hacer de dos maneras: por comprensión o por enumeración.
Para denotar un conjunto por comprensión, seleccionamos una propiedad que sea poseída por todos los elementos del conjunto y únicamente por ellos. De este modo podemos hablar del conjunto de los números naturales menores de 6, del conjunto de los satélites de la Tierra o el conjunto de los filósofos atenienses que formaron parte de una tiranía en el siglo V a. C. La notación utilizada para referirnos a los conjuntos por comprensión es la que sigue:
{x: x es un número natural menor que 6}
{x: x es un satélite de la Tierra}
{x: x es filósofo ateniense que formó parte de una tiranía en el siglo V a.C.}
Para denotar un conjunto por denotación hemos de nombrar cada uno de los elementos del conjunto. De este modo,m los conjuntos anteriores nombrados por extensión serían el conjunto cuyos elementos son el 0, 1, 2, 3, 4 y 5; el conjunto cuyo elemento es la Luna y el conjunto cuyo único elemento es Platón. Estos conjuntos se denotan, formalmente, como sigue:
{0, 1, 2, 3, 4, 5}
{la Luna}
{Platón}
Del conjunto cuyo único elemento es la Luna, decimos que es el conjunto unitario de la Luna, igual ocurre con el conjunto cuyo único elemento es Platón, del que también decimos que es el conjunto unitario de Platón.
Bibliografía:
BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.
