Curso de lógica (XI): teoría de conjuntos (V). Operaciones con conjuntos (II): complementación
En un post anterior de nuestro curso de lógica demostramos que el universo no es un conjunto, es decir, que no existe un conjunto de todos los objetos. Ahora bien, esto no representa ningún problema pues, en la práctica rara vez nos interesamos en todos los objetos del universo, sino solo en un dominio. Cuando hablamos de las elecciones, por ejemplo, estamos interesados en los votantes. En este sentido, cuando nos interesamos por un determinado dominio del universo, fijamos un conjunto, es decir, el conjunto de elementos que nos interesan en función del dominio del universo del que queremos hablar. A este conjunto lo llamamos universo del discurso y se denota mediante la letra «U». Este contiene todos los objetos por los que estamos interesados, aquellas cosas de las que hablamos en un determinado contexto. En este caso, también estaremos interesados en determinados conjuntos, a saber, los subconjuntos de U.
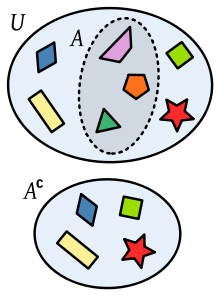
Representación del complemento mediante diagramas de Venn. Utilizan una notación diferente a la nuestra.
Bien, de este modo, dado un conjunto U y un subconjunto de U, el conjunto A, existe otro conjunto cuyos elementos son aquellos elementos de U que no forman parte de A. A este conjunto lo llamamos conjunto complementario de A con respecto a U y lo representamos así: ÃU. Nótese que ÃU = U – A.
Por otra parte se ha de tener en cuenta que no existe el complemento absoluto de un conjunto, es decir, hablar del complemento de un conjunto solo tiene sentido para un universo del discurso determinado. De este modo, si hubiera un conjunto que contuviera todos los elementos que no están en A, lo que hemos llamado el «complemento absoluto de A» y aplicáramos la unión entre ese conjunto y A, obtendríamos un conjunto universal, el cual, como se demostró en una entrada de este curso de lógica, no existe.
El complemento de un conjunto (en adelante omitiremos hablar del complemento de un conjunto respecto a U y omitiremos la U al lado de Ā para representar al complemento. Así, ÃU = Ã) tiene, al igual que otros conjuntos, una serie de propiedades. A continuación las enumeraremos.
1. El conjunto vacío y el universo del discurso son mutuamente complementarios.
2. Todo conjunto es el complemento de su propio complemento.
3. A ∩ Ã = U.
4. Si X es un subconjunto de U tal que A ∩ X = Ø entonces X ⊆ Ã.
5. A ∪ Ã = U.
6. Si X es un conjunto tal que A ∪ X = U, entonces à ⊆ X.
7. Ã es el único conjunto de X tal que (i) A ∩ X = Ø y (ii) A ∪ X = U
8. A ⊆ B si y solo si ~B ⊆ Ã.
9. A = B si y solo si ~B = Ã.
10. A ∩ B = Ø si y solo si A ⊆ ~B.
11. A ∪ B = U si y solo si à ⊆ ~B.
12. A – B = A ∩ ~B.
13. ~(A ∩ B) = Ã ∪ ~B.
14. ~(A ∪ B) = Ã ∩ B
15. A ∩ B = ~(Ã ∪ ~B).
16. A ∪ B = ~(Ã ∩ ~B).
Bibliografía:
BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.
