Curso de lógica (XIV). Teoría de conjuntos (VIII): operaciones con relaciones
En el último post dedicado a nuestro curso de lógica introdujimos una nueva noción de la teoría de conjuntos: las relaciones. Hoy profundizaremos algo más en ellas. De este modo, lo primero que vamos a hacer es presentar tres conjuntos nuevos que se pueden extraer de toda relación. Después, en segundo lugar, veremos algunas operaciones con relaciones. Esto nos será útil para el estudio de las funciones, que lo dejaremos para el siguiente post de nuestro curso de lógica dedicado a la teoría de conjuntos.
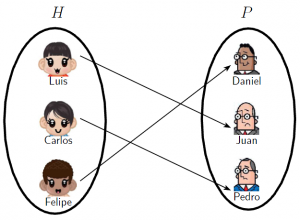
Dominio, recorrido y campo de una relación
Dada una relación R, el dominio de R, dom(R), es un conjunto formado por los primeros elementos de los pares de R. Su recorrido, rec(R), es el conjunto formado por los segundos elementos de R. Finalmente, el campo de R, campo(R), es la unión de su dominio y su recorrido o, lo que es lo mismo, el conjunto formado por todos los componentes de los pares de R. Así, dado un objeto a,
a ∈ dom(R) si y solo si hay algún objeto b tal que aRb.
a ∈ rec(R) si y solo si hay algún objeto b tal que bRa.
a ∈ campo(R) si y solo si hay algún objeto b tal que aRb o bRa.
Dado un conjunto A, decimos que R es una relación en A si R es un conjunto de pares ordenados de elementos de A. Es decir, R es una relación en A si y solo si R ⊆ A x A.
Operaciones con relaciones
Cuando realizamos cualquiera de las operaciones con conjuntos utilizando conjuntos de pares ordenados, obtenemos como resultados conjuntos de pares ordenados. Esto se aplica por igual para la unión, la intersección y la diferencia. De este modo, dadas las relaciones R y S, los conjuntos R ∪ S, R ∩ S, R – S y S – R también son relaciones. Por su parte, dados dos objetos a, b,
(a,b) ∈ R ∪ S si y solo si (a,b) ∈ R o (a,b) ∈ S.
(a,b) ∈ R ∩ S si y solo si (a,b) ∈ R y (a,b) ∈ S.
(a,b) ∈ R – S si y solo si (a,b) ∈ R y (a,b) ∉ S.
(a,b) ∈ S – R si y solo si (a,b) ∉ R y (a,b) ∈ S.
O también,
a(R ∪ S)b si y solo si aRb o aSb.
a(R ∩ S)b si y solo si aRb y aSb.
a(R – S)b si y solo si aRb y no aSb.
a(S – R)b si y solo si no aRb y aSb.
Si una relación R se da entre dos objetos a y b, aRb, se puede obtener una relación entre b y a, a la que llamamos relación inversa de R, ~R. Expresado con mayor precisión:
~R = {(x,y) : (y,x) ∈ R}
De este modo, dados dos objetos a y b, a~Rb si y solo si bRa.
Por último, dadas dos relaciones R y S se puede obtener una nueva relación a partir de estas a la que llamamos producto relacional, R|S. Este se define como sigue:
R|S = {(x,y) : hay algún z tal que (x,z) ∈ R y (z,y) ∈ S}
De este modo, dados los objetos a,b,
a(R|S)b si y solo si hay algún objeto z tal que aRz y zSb.
Bibliografía:
BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.
