Curso de lógica (XIII). Teoría de conjuntos (VII): pares ordenados, relaciones y producto cartesiano
Llevamos varias semanas con nuestro fabuloso curso de lógica aparcado y esto es inadmisible. Y como somos conscientes de la inadmisibilidad de tal cosa hemos decidido retomarlo hoy. En la entrada anterior hablamos sobre el conjunto potencia y sobre la existencia de conjuntos. Hoy daremos un paso más en términos de complejidad, profundizando más en la teoría de conjuntos. Veremos los pares ordenados y las relaciones.
Introducción: el orden de las relaciones
En teoría de conjuntos existe, como es natural, la irremediable costumbre de hablar sobre conjuntos y sobre los elementos de estos. Hemos aprendido como el principio de separación nos permite utilizar el lenguaje de la teoría de conjuntos para hablar de las propiedades de un conjunto dado. Sin embargo, ocurre que algunos elementos de algunos conjuntos están en una relación determinada con otros elementos. Es el caso del conjunto de los números naturales, en el que el 1 y el 2 caen bajo la relación «_es el sucesor de_». ¿Cómo expresamos las relaciones en teoría de conjuntos? Antes de nada conviene observar que las relaciones tienen un orden o una dirección. En efecto, en el caso de nuestro ejemplo, una de las relaciones entre el 1 y el 2 es que el 2 es sucesor del 1. Si cambiamos la posición del 1 con la del 2 observamos que esa relación (el 1 es sucesor del 2) no se da en el conjunto de los números naturales. Para expresar el orden de las relaciones se introduce el concepto de par ordenado. Con ayuda de pares ordenados se puede formular una teoría de las relaciones.
Pares ordenados
Un par ordenado es una función que nos permite distinguir un primer componente de un segundo componente. Es un nuevo conjunto creado a partir de dos elementos de ese conjunto que caen bajo una relación. Así, el par ordenado de a y b es el conjunto
(a,b) = {{a},{a,b}}
Al elemento que aparece a nuestra izquierda, a en este caso, lo llamamos primer componente del par ordenado (a,b). Al que aparece a nuestra derecha, b, lo llamamos segundo componente del par ordenado (a,b).
Relaciones
Las relaciones de un conjunto dado son conjuntos de los pares ordenados de dicho conjunto. Para expresar las relaciones utilizaremos las letras «R», «S» y «T», serán variables de relaciones. Para expresar que una relación dada, R pongamos por caso, se da entre dos elementos de un conjunto lo haremos así: aRb o de este otro modo: (a,b) ϵ R , que se lee como «a está relacionado con b por R» o R se da entre a y b. Cuando queramos expresar que dos elementos de un conjunto no caen bajo la relación R, entonces lo haremos así: (a,b) ∉ R. En este caso se lee «a no está relacionado con b (por R)» o «R no se da entre a y b».
De este modo, para definir por ejemplo la relación de sucesión, dentro de los números naturales, diremos que esta es el conjunto de los pares ordenados (a,b) tales que a es sucesor de b. Así, si llamamos a esta relación S, entonces S es el siguiente conjunto:
S = {(1,0),(2,1),(3,2)…(n+1,n),(n+2,n+1)…(n+n+1,n+n)}.
Producto cartesiano
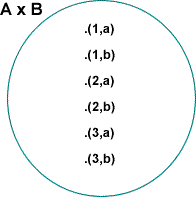
Vistos los pares ordenados y las relaciones conviene que introduzcamos una nueva operación entre conjuntos: el producto cartesiano. Dados dos conjuntos A y B, el producto cartesiano de A y B, A x B, es el conjunto de los pares ordenados tales que el primer componente del par es un elemento de A y el segundo un elemento de B. De este modo,
Si A = {a,b,c} y B = {d,c,e}, entonces A x B = {(a,b),(a,c),(a,e),(b,a),(b,c),(b,e),(c,a),(c,c),(c,e)} y B x A = {(d,a),(d,b),(d,c),(c,a),(c,b),(c,c),(e,a),(e,b),(e,c)}
Cuando uno de los conjuntos es vacío, entonces el producto cartesiano es también vacío. Así:
Si A = Ø o B = Ø, entonces A x B = Ø y B x A = Ø.
Además, como se ve en el ejemplo anterior, el producto cartesiano no es conmutativo, es decir
A x B ≠ B x A
Ahora bien, si A = B, entonces A x B = B x A. Con un ejemplo:
A = {1,2} y B = {1,2} entonces A x B = {(1,1),(1,2),(2,1),(2,2)} y B x A = {(1,1),(1,2),(2,1),(2,2)}
