Curso de lógica (XII): teoría de conjuntos (VI). Conjunto potencia. Existencia de conjuntos
Lo último que vimos en nuestro curso de lógica fue la complementación. En este apartado hablaremos sobre la existencia de conjuntos, una vez que hayamos visto el conjunto potencia. Pasaremos a ello si más ambages.
El conjunto potencia es un conjunto cuyos elementos son subconjuntos.
El conjunto potencia
Dado un conjunto A, existe un conjunto cuyos elementos son todos los subconjuntos de A. Este es el conjunto potencia, en símbolos Ƥ(A). De este modo, Ƥ(A) = {x: x ⊆ A}. El conjunto potencia es un conjunto de conjuntos, es decir, un conjunto cuyos elementos son conjuntos. A continuación veremos algunos ejemplos de conjuntos potencia:
Ƥ(∅) = {∅}
Ƥ({a}) = {∅,{a}}
Ƥ({a,b}) = {∅,{a},{b},{a,b}}
Ƥ(a,b,c} = {∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}
Además en la siguiente tabla relacionaremos los anteriores conjuntos en relación con sus respectivos conjuntos potencia, tomando el número de sus elementos como criterio. Desde esta perspectiva, obtendremos una serie de observaciones sobre las propiedades del conjunto potencia de un conjunto dado.
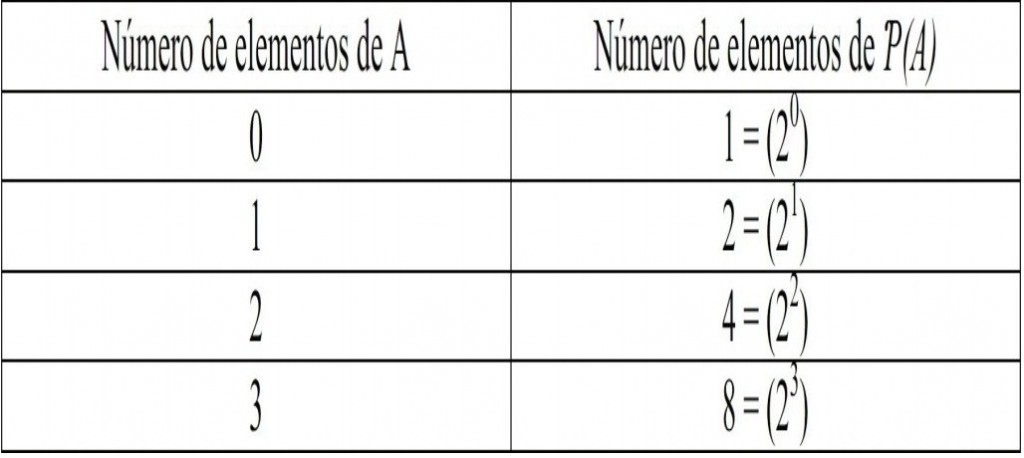
Las observaciones que se pueden hacer aquí son las siguientes:
1. Ƥ(A) siempre tiene más elementos que A.
2. ∅ es un subconjunto de todo conjunto. ∅ siempre forma parte de Ƥ(A).
3. Si A tiene n elementos, entonces Ƥ(A) tiene 2 elevado a n elementos.
4. Si tenemos en cuenta la definición de conjunto potencia, entonces dados un conjunto A y un conjunto X, X ∈ Ƥ(A) si y solo si X ⊆ A.
5. Para todo objeto a, a ∈ A si y solo si {a} ⊆ A, por tanto a ∈ A si y solo si {a} ∈ Ƥ(A).
7. Para todo conjunto A, A ∈ Ƥ(A) y ∅ ∈ Ƥ(A).
Introducción a las relaciones
Como dijimos en otro lugar, los objetos abstractos son ficciones útiles, se postulan porque en la práctica prestan algún servicio. Los conjuntos son objetos abstractos. Hasta ahora hemos hablado de diversos conjuntos, tales como el conjunto vacío o el conjunto potencia. La existencia de estos conjuntos viene garantizada por los axiomas de la teoría de conjuntos (la teoría de conjuntos es una teoría axiomática). Sin embargo, desde que comenzamos con la teoría de conjuntos en nuestro curso de lógica solo hemos mencionado dos de estos axiomas o principios, a saber, el axioma o principio de extensionalidad y el axioma de separación. El primero no garantiza la existencia de ninguno de los conjuntos de los que hemos hablado; por su parte, el axioma de separación garantiza la existencia del conjunto vacío, como vimos en su momento en nuestro curso de lógica. A continuación enumeraremos algunos de los axiomas en los que se basa el trozo de teoría de conjuntos que veremos aquí.
1. Axioma de no vacuidad: existe un conjunto por lo menos.
2. Axioma de separación: dados los objetos a y b, existe un conjunto, {a,b}, cuyos elementos son a y b.
La teoría de conjuntos se compone de varios axiomas más. Los axiomas de extensionalidad, de separación, del conjunto potencia, de la unión y de infinitud no han sido mencionados aquí. Los dos primeros han sido ya comentados en otras entradas anteriores. Por su parte, el axioma del conjunto potencia aparece más arriba. En cuanto al axioma de la unión y de la infinitud, no los veremos aquí, ya que la parte de la teoría de conjuntos que veremos en este curso de lógica es únicamente la necesaria para introducirnos en la lógica de predicados de primer y segundo orden.
Bibliografía:
BADESA, C., JANÉ, I., JANSANA, R. Elementos de lógica formal. Ariel Filosofía, 2000. Barcelona.

